

The World of Orthocenters
An Exploration of Different Orthocenter Constructions
by
Sarah Major
This write-up is based on the constructions from the beginning of Exploration 8, which are as follows:
Perform the following constructions
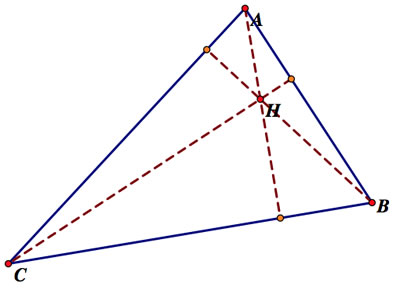
a. Construct any triangle ABC.
b. Construct the Orthocenter H of triangle ABC.
c. Construct the Orthocenter of triangle HBC.
d. Construct the Orthocenter of triangle HAB.
e. Construct the Orthocenter of triangle HAC. f. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
First, we will construct the original orthocenter H for triangle ABC:

This first thing we notice while doing these constructions is that when constructing the orthocenters involving the original orthocenter, the new orthocenter is the left over vertex. That is, the orthocenter is the vertex of the original triangle that is not contained in the triangle in which we are constructing the orthocenter.
For triangle HBC, the orthocenter is A.

For triangle HAB, the orthocenter is C.

For triangle HAC, the orthocenter is B.

Why is this? The orthocenter is constructed from the altitudes of a triangle. That is, this point is constructed by the segments extending from the vertices to the opposite sides, and these segments are perpendicular to the corresponding opposite side.
These altitudes actually split the triangle into the three other triangles that we constructed. Therefore, the original orthocenter is now one of the vertices of each of the new triangles, and the new altitude created by this vertex lies on the original altitude passing through the orthocenter.
This is why the orthocenters of the new triangle lie on the same altitude segments as the original triangle. The new altitudes formed lie on the old altitudes.
But why are the orthocenters of the new triangles the exact vertices of the original triangle? One obvious reason is that the new triangles share one of the sides of the original triangle. Therefore, we know that the orthocenter will at least lie on the line corresponding to the segment formed by the altitude formed by this side, which we have already shown.
What about the other new altitudes? Why do these pass exactly through the point that is the original vertex? Like previously stated, the altitudes are perpendicular to the sides of the triangle. The original altitudes are, of course, perpendicular to the sides of the original triangle. The new triangles are formed by these altitudes. When constructing the new altitudes, they are perpendicular to the new triangle sides, and thus, perpendicular to the segments that are perpendicular to the original sides. A segment that is perpendicular to a segment that is perpendicular to another line is thus parallel to the original line. Therefore, the new altitudes are parallel to the sides of the original triangle. In fact, the altitudes lie exactly on the original sides of the triangle because these are the only segments that can be parallel to these original sides and still pass through the new orthocenter (or original vertex) of the triangle (note that the new altitudes are red):
As the above images show, the segments that are parallel to the sides of the original triangle and pass through the original vertices must be the sides of the original triangle. The only point that contains both the two sides of the original triangle and the perpendicular line of the other side must be the original vertex.
What if one of the sides of the original triangle was moved to where the original orthocenter is? How would the construction change?
To view this in GSP, I used the same construction but used a coordinate plane to see what the coordinates of the points where. When I moved the points, I made sure that when I moved the vertex of the original triangle, it was the same coordinate as the original orthocenter. Unfortunately, I found it difficult to get the coordinates to be the exact same, but they were close enough to tentatively infer results.
I chose to move the orthocenter of triangle HAB to the location of the original orthocenter. In doing so, I can safely say that though I was not able to move the point to the exact intentional location, the original orthocenter should be in the location of the original vertex. This is the same case for moving any of the original vertices.
Why is this? Essentially, it’s for the same reason as we previously discussed. The altitude for the side that is shared by the original triangle and the new triangle is the same, so the altitude formed by the side that is the same will lie on the same line for both the original triangle and the new triangle. Therefore, both the orthocenter and the opposite vertex will lie on the same line. The other vertices are staying the same, so the altitudes of the new triangles and the sides of the original triangle are the same. Therefore, when we move a vertex of the original triangle to the location of the original orthocenter, we’re simply switching the orthocenter of the original triangle with the orthocenter of the new triangle.
If we draw the circumcircles of the original triangle and the new triangles, we can see that this is the case because the circles are simply being switched.
This is because for every triangle, there can be one and only one circumcircle. This is because the circle passes through all three of the vertices of the triangle. Therefore, only one circle can pass through all three of these points. If we switch the points and the new circumcenter is the same as the old one, the new vertices must be the same as the original triangle.
What if, instead of using circumcircles, we use the nine point circle for each of the triangles?

The nine point circle is the same for all of the triangles, including the original triangle. Not only that, but the nine points are also the same for all of the triangles.
Why is this? Well, what are the points of the nine point circle? Three are the midpoints of the sides of a triangle, three are the midpoints of the segments extending from the orthocenter to the vertices of the triangle, and three are the feet of the altitudes. Let's focus on the original triangle and one of the new triangles, HAB, to show how these nine points are the same for both triangles.

As previously shown, the altitudes of the new triangle extending from the orthocenter lies on the original triangle's altitude. Therefore, the foot of this altitude will be the same for both triangles.

The two triangles share a side, so the midpoint of this side will certainly be the same point.

The other two sides of the original triangle are actually the other two altitudes of the new triangle, so the midpoints of these two segments will lie on the same point.

The segments forming the two sides of the new triangle that are not in common with the original triangle are actually the segments extending from the orthocenter to the vertices, so these midpoints will lie on the same points for both triangles.

The is one segment extending from the orthocenter to the vertex of a triangle that has not been accounted for both the new and original triangle. However, this is actually the same segment for both triangles. C is the vertex of the original triangle while H is the orthocenter. The reverse is true for the new triangle. Therefore, the midpoint of this segment is the same for both triangles.

The tricky part is finding the last two points because they are hard to explain. We haven't accounted for the feet of the other two altitudes of the new triangle because they are actually contained on the sides of the original triangle. However, an altitude actually extends from the vertex of a triangle to the opposite side. The point at which the altitude meets this side is called the foot of the altitude. To find the the feet of the other two altitudes, we have to extend the other two sides of the triangle. We then find these two points.

But how do these two points correspond to the original triangle? Well, we essentially just found the two feet of the other two altitudes for the original triangle by extending the original altitudes to their original length. These two points are actually the feet of these altitudes. Therefore, we have found the nine points of the nine point circle, and they are the same for both the original triangle and the new triangle. We could do the same for the other two smaller triangles and find the same exact points.